領域内高速塗りつぶし法 / High-speed Region Fill Method

テ～マ

図１のような閉じた領域の内部を高速に塗りつぶすアルゴリズムと、プログラム例を示す

Why?

かつて作っていた『お絵描き掲示板』に、「塗りつぶし」コマンド（＝お絵描きソフトで、ペンキ缶のアイコンのやつ） をつけようかなと思い、そのやり方を考えてみました。そしたら、とてもいいロジックが出来たので紹介することにしました。このロジックは、私が今まで調べたもののうち、どんなものよりも高速で、 かつ単純なものになっています。
（ただし、これは2000年ごろに作ったものですし、もっと速いやり方があるかもしれません！）。

ではさっそくそのロジック（アルゴリズム）を説明します。

原理

一般的な塗りつぶしのアルゴリズムは以下のようなもの。
これは、走査線一本ごとに境界を探して行く方法なので、 「スキャンラインアルゴリズム」とか「走査線アルゴリズム」とか呼ばれている。

処理ステップ

前提として、図２のような、閉曲線（境界線）で囲まれた領域があるとする

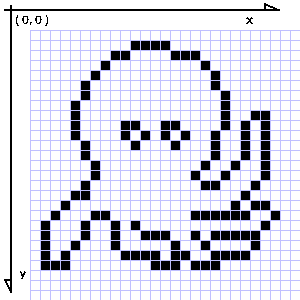
0. まず塗りつぶしを始める一点 ( X, Y ) を決める
1. その座標 X, Y をスタックに積む
2. スタックから座標 X , Y を取り出す
3. ( X, Y )から左に１ピクセルずつ調べ、初めて境界のピクセルになる１個前のｘ座標 Xleft を取る
4. 同様に( X, Y )から右に１ピクセルずつ調べ、右の境界の１ピクセル前のｘ座標 Xright を取る
5. ( Xleft, Y-1 )から( Xright, Y-1 )まで１ピクセルずつ調べる。この区間には境界線が含まれる 可能性がある。境界線が含まれていた場合、領域の内部から境界のピクセルに入る直前のピクセルの座標 ( Xin, Y-1 ) をスタックに積む。この区間には複数の Xin が含まれている可能性があるが、それらの座標を全てスタックに積む。
6. ６と同様にして、( Xleft, Y+1 )から( Xright, Y+1 )まで１ピクセルずつ調べ、見つかった全ての( Xin, y+1 )をスタックに積んでいく
7. スタックが空になるまで、３に戻って処理を続ける

しかし、このアルゴリズムにはとても無駄が多い（図３参照）。

無駄１

３－＞４－＞５の手順で、すでに「境界は含まれていない」と分かっているはずの区間を調べてしまう

無駄２

６、７の処理も、すでに調べた区間を調べなおしてしまう

 

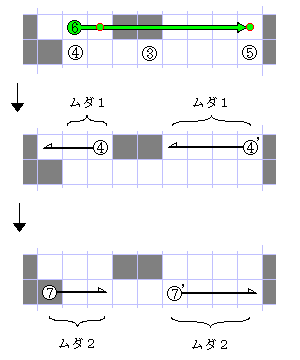
たとえばｘ、ｙ軸に平行な辺をもつ単純な長方形の内部を塗りつぶす場合、 無駄１を省くだけで計算量は半分になり、無駄２を省けばさらに半分になる。 つまりこの２つを省けば１／４の計算量ですむことになる。
複雑な図形を塗りつぶす場合は、これらの無駄を省くことでさらに大幅な計算量の削減ができることになる。

以下に、その無駄を省く、かっちょいいアルゴリズムを示す

無駄を省くアルゴリズム

無駄１、２を省くには、８つのパターンを導入すればよい。
これによって「一度行った計算は二度行わない」ことが徹底され、 また、同時に無駄１、２を省くことができるので、 それぞれの無駄を別個に省くよりもはるかに効率がよくなり、 同時にアルゴリズムも読みやすくなる。 また、座標と同時に６種のパターンのうちひとつをスタックに積むだけなので メモリもほとんど食わないという利点がある。
これよりいいアルゴリズムがあったらば教えて欲しいってぐらいグッドなアイデアだ。 （自画自賛）
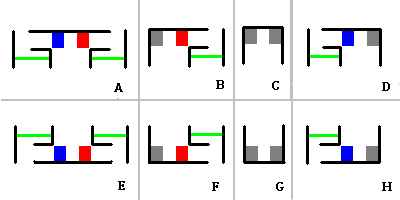
その８つのパターンとは、以下のものである（図４）。それぞれに識別子としてアルファベットのＡ～Ｈを割り振ってある（実際には、識別に３ビットだけ割り振ればよい）。

 

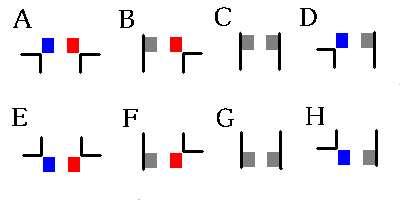
図で、黒の線は境界線（壁）を表す。
上下方向がｙ軸方向、左右方向がｘ軸方向で、下向きを正、右向きを正とする。
青、赤、灰色の四角は、１ピクセルを示している。これらは領域内のピクセルである。
Ａ，Ｂ，Ｃ，Ｄでは、ピクセルがある位置のｙ座標（ｙ－１）と、 その一つ下の（ｙ）の座標との関係が示されている。
Ｅ，Ｆ，Ｇ，Ｈでは、ピクセルがある位置のｙ座標（ｙ＋１）と、 そのひとつ上の（ｙ）座標との関係が示されている。

四角形の色は、無駄１を省くことに関係している。
青い四角は、左に１ピクセルずつ調べて左の境界を調べる必要があることを示し、 赤い四角は同様に、右に１ピクセルずつ調べて右の境界を調べる必要があることを示している。
また、灰色の四角は左（右）の壁にひっついていて、これ以上左（右）にピクセルを調べる必要がないことを示す。

ここで、どのように無駄１が省かれるかを説明しよう。

無駄１を省くテクニック

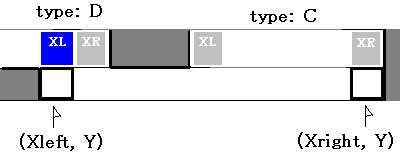
処理ステップ６を行う段階で、( Xleft, Y-1 )から( Xright, Y-1 )までを調べるが、 そのときに、１ピクセルずつ境界かどうかを調べるので、この情報を図５や図６の ようにして、境界のまわりの座標 ( XL, Y-1 ) , ( XR, Y-1 ) とタイプを保存しておく。
そうすると次に来る４，５でもう一度無駄な計算をせずに済むことになる。
４の処理において、タイプＢまたはＣならば XL から左に調べる必要がないことになる。
５の処理において、タイプＡならXRまで調べなくていいし、タイプＣまたはＤなら右に調べる必要がないということになる。

 

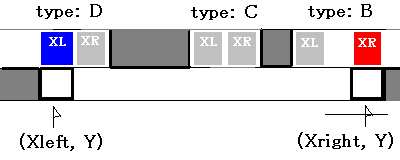
無駄１を省くだけなら、パターンは４種類で足りることになる。
パターンが８種類あるのは無駄２を省くことと関係している。

次に無駄２がどのように省かれるかを説明しよう。

無駄２を省くテクニック

図７は無駄２を省くための模式図である。
図７の緑の線は、処理ステップ６，７でそれぞれ調べなくてはいけない領域をしめしている。逆に言うと、緑の線が無い領域は調べなくてよいというのが分かっている領域ということになる。つまり、パターンを調べることで、無駄２を省くことができることになる。

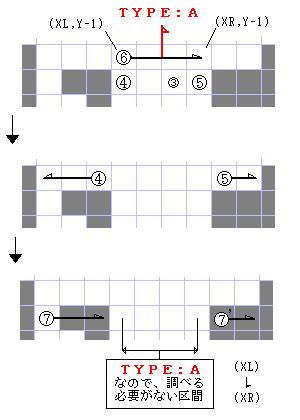
これだけでは分かりにくいので、図８を参照してほしい。
処理ステップ６が終了した時点で、まずＡ～Ｄのパターンのどれに当てはまるかが分かる。 図では、パターンＡである （ステップ７を行う時点ではＥ～Ｆのパターンのうちどれかが当てはまる）。
さらに処理が進み、また処理ステップ４，５を通過してステップ７に来たとき、パターンＡという情報が、( XL, XR )という座標と共に残っているので、これによって先ほど調べたはずの領域を省くことができるようになる。

 

以上で、アルゴリズムについての説明は終わりです。
この考え方を用いたサンプルプログラムを用意しました。

サンプルプログラム

Java アプレット版

*coming soon